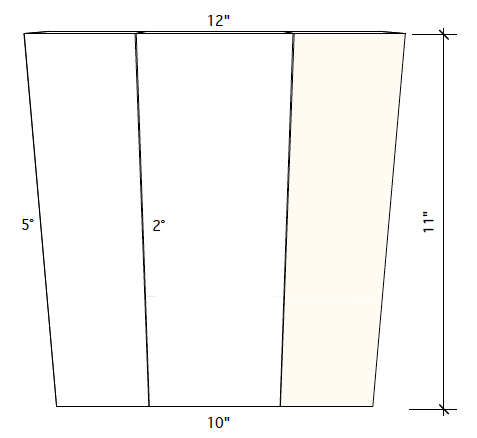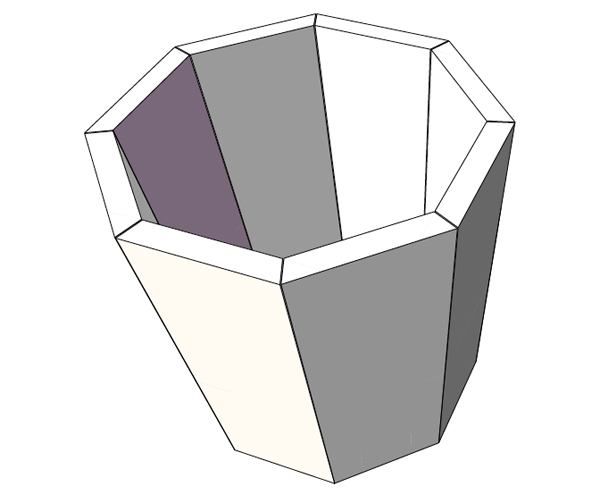
I would like to build an octagon (eight-sided) bucket for my outdoor wishing well. I have tried 22-1/2 degrees, but the parts do not mesh properly. How do you figure out the compound angle? The bucket would be 11 inches high, 12 inches across the top flats, and 10 inches across the bottom flats. – Stanley J. Kozak
Chris Marshall: Stanley, welcome to the wild and often frustrating world of compound angles. To make matters worse, they’re even more challenging when you’re trying to join multiple pieces of wood together in a closed form like your bucket. So, the bucket pieces don’t fit together? I’m not surprised one bit – and I’d be in the same boat with you. There are a couple of big variables here. First, is the geometry right? And second, is your table saw yielding the accuracy you need to make these super-precise cuts?
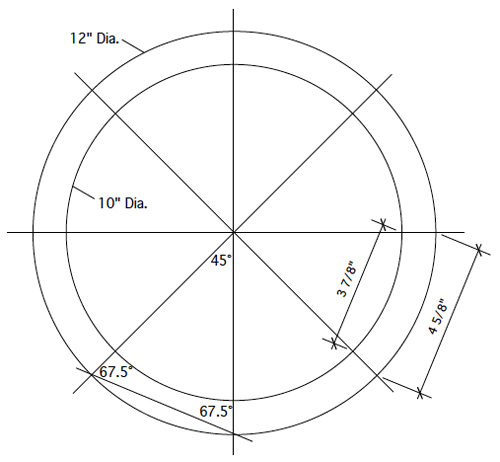
To the first question, have a look at the “pie” illustration below. An octagon forms eight interior isosceles triangles with vertex angles (the ones closest to the center) that each measure 45 degrees. Since the sides of these triangles match one another, their base angles have to match, too. And, we know that the interior angles of a triangle add up to 180 degrees. So, 180 minus 45 equals 135 remaining degrees for each triangle. Divide that by two, and you end up with 67.5 degrees. The complementary angle (and what you’re tipping your saw blade to for the bevel cuts) is, in fact, 22.5 degrees. You’re right on the money there.
But, there’s another important angle here, too, making things compound. Each of the trapezoids that form your bucket have sides that taper from top to bottom. According to a quick CAD sketch, a bucket 11 inches tall with a rim diameter of 12 in. and a base diameter of 10 inches would have “staves” that taper from 4-5/8” at the top to 3-7/8” at the bottom. Those taper angles are approximately 2 degrees.
Here’s the machine side of the quandary: In order for your bucket pieces to fit together, the bevel tilt of the blade has to be precisely 22.5 degrees. If the blade is off by even a few tenths of a degree, the error compounds around the octagon and the pieces won’t come together and close properly. The 2-degree ripping angle of the staves is important, too. A degree or two off here won’t allow the joints to close, either.
My suggestion is to carefully check your saw settings. Are your rip cuts actually forming 2-degree tapers on the workpiece edges? Is the blade tilt exactly 22.5 degrees? More than likely, your error is happening at the saw. It’s probably not your math. Good luck, and keep trying! And look on the bright side: here’s a good excuse to cull the scrap bin by making lots and lots of test cuts.